ואולם, מסתבר שלא רק מוטציות מאפשרות לחיידקים לשרוד בנוכחות אנטיביוטיקה. באוכלוסיית החיידקים קיימת שונוּת טבעית, שבזכותה לפחות חלק מהחיידקים שורדים בנוכחות אנטיביוטיקה, אף כי אין הבדל גנטי בינם לבין שאר האוכלוסייה. קבוצת חוקרים מן האוניברסיטה העברית, בראשותה של ד"ר נטלי קסטמבר-בלבן מהמחלקה לפיזיקה ביולוגית, עוסקת בניתוח מתמטי של התנהגותן של אוכלוסיות חיידקים בהשפעת אנטיביוטיקה. הקבוצה, הכוללת את ד"ר חנה גבאי, אורית גפן, אורי ג'יוון, איתן רותם, סיוון פרל ודוד שבא, מבצעת הן את הניסויים הביולוגיים עצמם, והן התאמת מודלים תיאורטיים לתוצאות הניסויים. נוסף על העבודה המוצגת כאן, עוסקת הקבוצה בהיבטים נוספים של שונות באוכלוסיות של חיידקים ושמרים, ובהם ההיבט האבולוציוני, שאותו נוח במיוחד לחקור בחיידקים, הודות לקצב הריבוי הגבוה שלהם.
אם נתבונן באוכלוסיית חיידקים זהים מבחינה גנטית הנחשפת לאנטיביוטיקה, ניווכח כי במקרים רבים חיידקים אחדים ממשיכים להתקיים לאחר מותם של רוב האחרים. החיידקים שנותרו ימותו אף הם בהדרגה, אך בקצב אטי בהרבה. חיידקים "שורדים" אלה עשויים להישאר בחיים במשך פרק הזמן המומלץ לטיפול אנטיביוטי. שרידות זו נובעת, ככל הנראה, מכך שהחיידקים נמצאים בשלב רדום בהתפתחותם. האנטיביוטיקה פוגעת בעיקר בתאים פעילים ומתחלקים; אם חיידקים מסוימים אינם מתחלקים, או עושים זאת בקצב אטי מאוד, הם עשויים שלא להיפגע מהאנטיביוטיקה במשך כל תקופת הטיפול. חיידקים אטיים, או "רדומים", אלה אינם שונים, גנטית, מן החיידקים הנורמליים. בתדירות מסוימת, חיידקים עוברים באופן ספונטני מאוכלוסייה אחת לאוכלוסייה אחרת: חיידק "רדום", או אטי, יכול "להתעורר" ולהפוך לפעיל, ופעיל יכול להפוך לאטי. ההסתברויות, או קבועי הזמן האופייניים למעברים אלה, הם הפרמטרים שמתארים את הדינמיקה של המערכת.
קיומן של פאזות שונות (נורמלית ואטית) באוכלוסייה בעלת מטען גנטי אחיד מקנה לה יתרון אבולוציוני בסביבה משתנה. בתנאים מסוימים, חיידקים המתרבים במהירות הם בעלי יתרון הישרדותי; בתנאים אחרים, כמו בחשיפה של ימים אחדים לאנטיביוטיקה או לתנאים קיצוניים אחרים, ישרדו דווקא חיידקים שקצב התחלקותם נמוך. אם הסביבה קבועה, או משתנה באופן סדיר, קיים דפוס תגובה יחיד אופטימלי, אולם אם הסביבה משתנה באופן בלתי צפוי, יש יתרון גדול לאי-אחידות באוכלוסייה.
על מנת לבחון את הקשר בין שרידותם של החיידקים לבין קצב ההתרבות שלהם, החוקרים מגדלים חיידקים על מצע הבנוי מתעלות זעירות (ראו תמונה). כאשר חיידק מתחלק ומתרבה, האוכלוסייה בתעלה שבה הוא נמצא גדלה, ואפשר לעקוב אחר גידולה במיקרוסקופ. החוקרים חושפים את האוכלוסייה לאנטיביוטיקה, לאחר זמן קצוב מסלקים את האנטיביוטיקה, ואז שבים ומוסיפים אנטיביוטיקה וחוזר חלילה. במהלך שינויים אלה צופים החוקרים באוכלוסיית החיידקים בכל אחת מן התעלות, ועוקבים אחר קצב התחלקותם ותמותתם. לשם כך הם מקפידים על חשיפה מבוקרת ואחידה לכל החיידקים, ומקיימים צפייה מיקרוסקופית מתמשכת ומדויקת בחיידקים בודדים. כך הם יכולים לראות אם החיידקים השורדים הם אותם חיידקים אשר מלכתחילה לא התרבו בקצב מהיר.
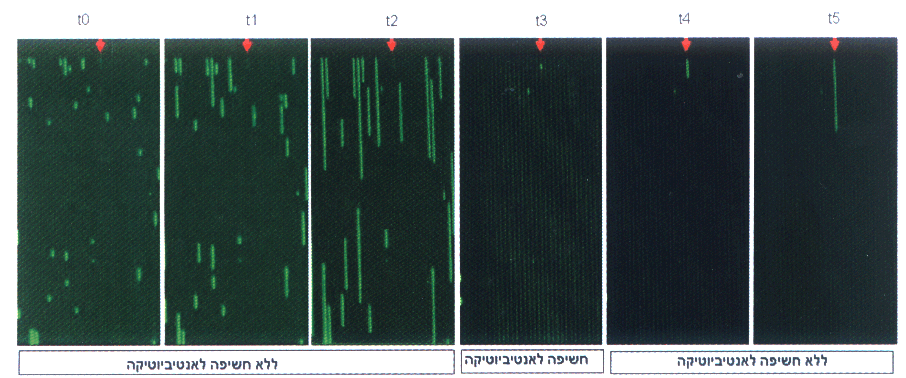
החיידק הנמצא בתעלה המסומנת בחץ אדום, שהיה בשלב אטי (רדום), בעת החשיפה לאנטיביוטיקה (אפשר לראות כי לא התחלק בזמנים t0, t1, t2), הוא ששרד במשך החשיפה לאנטיביוטיקה (t3). לאחר מכן החל להתרבות, וכך יצר אוכלוסיית חיידקים חדשה (t4, t5).
העבודה על הגבול בין פיזיקה לביולוגיה משלבת את השיטות, ולכן גם את הקשיים, של שני התחומים. החוקרים נדרשים לשליטה בשיטות שונות ורבות. אורית גפן, דוקטורנטית: "הניסוי מתחיל בבוקר ויכול להיגמר למחרת, ובמשך היום צריך לעקוב אחריו באופן מתמיד. לאחר מכן יש הרבה עיבוד תוצאות ממוחשב – מהמיקרוסקופ מתקבלות תמונות, שמהן צריך להפיק את המידע."
הביולוגיה הקלאסית עוסקת, במקרים רבים, בניסיון להבין כיצד מתרחשים תהליכים ברמה המיקרוסקופית. גם במקרה זה, מעניין לנסות להבין מהו המנגנון הקובע אילו מן החיידקים יהיו נורמליים, ואילו – אטיים. אך בד בבד, קיים מידע מעניין אחר, בעל אופי סטטיסטי, שאפשר לקבל כאשר עוסקים באוכלוסיות גדולות. גישה זו דומה במידה רבה לגישה העומדת ביסודה של המכניקה הסטטיסטית. במכניקה רגילה עוסקים במיקומו של חלקיק, במהירות שלו ובתאוצות המשפיעות עליו, ומכאן מקבלים מידע על מיקומו העתידי בזמן כלשהו. במכניקה סטטיסטית עוסקים במספר רב של חלקיקים. במקום להתייחס בנפרד למיקומו ולמהירותו של כל חלקיק, מגדירה המכניקה הסטטיסטית גדלים תרמודינמיים, כגון לחץ וטמפרטורה, המספקים מידע סטטיסטי משמעותי על כלל אוכלוסיית החלקיקים. גישה זו מאפשרת להימנע מעיסוק נפרד בכל אחד מהמוני חלקיקי הגז הנמצאים בבלון, ועדיין להבין כיצד הבלון מתנפח ומתי הוא עתיד להתפוצץ. גדלים כמו טמפרטורה ולחץ אינם נחוצים ואינם רלוונטיים לחלקיק בודד, אך כאשר אוכלוסיית החלקיקים גדולה דיה, הם הופכים להיות המתאימים ביותר לטיפול בבעיה. הגדלים התרמודינמיים, המשמשים לתיאור אוסף גדול של חלקיקים, מקיימים ביניהם יחסים מתמטיים המגדירים את הפיזיקה של המערכת.
החוקרים מהאוניברסיטה העברית מנסים להתאים לתמותת החיידקים מודלים מתמטיים של משוואות דיפרנציאליות פשוטות, הדומות לאלה המשמשות במערכות רבות בפיזיקה. הגדלים הסטטיסטיים הרלוונטיים הם קצבי המעבר של החיידקים מהאוכלוסייה הנורמלית לאטית, ולהפך. מבחינה תיאורטית, מדובר בתהליך של שבירת סימטריה: שני חיידקים בעלי אותו קוד גנטי, הנחשפים לסביבה זהה, מגיבים בצורה שונה. החיידקים שישרדו למרות האנטיביוטיקה יקימו דור נוסף שגם בו יתפלגו החיידקים לנורמליים ולאטיים, וגם בדור החדש יוכלו חיידקים לעבור באופן אקראי, אך לפי הסתברויות וקבועי זמן אופייניים, מאוכלוסייה אחת לאחרת. המתמטיקה שמתארת את המערכת היא מתמטיקה של תהליכים סטוכסטיים (אקראיים). מנקודת מבט זו, אנו מתעלמים מן התהליך המיקרוסקופי הגורם לחיידק יחיד, מסוים, להיות נורמלי או אטי. תחת זאת אנו עוסקים בהסתברויות ובקבועי זמן בעלי אופי סטטיסטי, הרלוונטיים לאוכלוסיות גדולות.
ואולם, טיפול סטטיסטי זה אינו מבטל את הצורך בחקירה מיקרוסקופית שתתעמק בטבע התהליכים. נטלי קסטמבר-בלבן: "הראינו שקצבי המעבר תלויים בסביבה. עכשיו צריך לעבור לרמת ה-DNA, ולראות איך הגנים שקובעים את התגובה לסביבה משפיעים זה על זה וקשורים בינם לבין עצמם. המשוואות המתארות את היחסים בין הגנים ברמה המיקרוסקופית צריכות להוביל למשוואות המתארות את ההתנהגות הנצפית ברמה המאקרוסקופית."